Triada Klagkou
Introducción
Desde la época de Platón hasta nuestros días, existe la opinión unánime de que la contribución de Pitágoras y de los Pitagóricos ha sido decisiva para el desarrollo de las matemáticas y de la música. La Escuela de Pitágoras es considerada como la primera Universidad del mundo.
Hagamos un pequeño recorrido por la ciencia actual con el fin de corroborar en ella el pensamiento pitagórico.
Kepler, pensamiento pitagórico, políedros platónicos
El astrónomo J. Kepler (1571 – 1630) consideraba, al igual que los Pitagóricos, que los números era apasionantes. Kepler insistía en que el universo físico estaba planificado de acuerdo a modelos matemáticos, las cuales eran simples y accesibles a la inteligencia humana.
Un cubo fantástico separaba a Saturno de Júpiter, un tetraedro regular se encontraba entre Jupiter y Marte, un dodecaedro regular separaba a Marte de la Tierra,
un icosaedro regular estaba entre la Tierra y Venus y un octaedro regular separaba a Venus de Mercurio.
Dirac y el pensamiento pitagórico. Belleza matemática
P. Dirac (1902 – 1984) es quien previó teóricamente la existencia de los anticuerpos. Al mismo tiempo, era inspirado por la idea de la belleza matemática. En
1963, en un artículo del Scientific American, dijo:
“Una teoría con belleza matemática es más probable que sea correcta que otra fea que sustente algún elemento matemático. Dios es un matemático de gran altura y utiliza unas matemáticas muy avanzadas en la estructuración del universo”.
La pérdida de la proporción original. Cambio de frecuencia original
La escala musical que introdujo Pitágoras en Occidente, y que utilizan los hindúes, comienza con la nota Do y su frecuencia es de 256 ciclos por segundo (Hertz).
Podemos verla representada incluso en dibujos de Robert Floudd, de la época del Renacimiento. Sin embargo, hoy hemos cambiado esta frecuencia y utilizamos para la nota Do la frecuencia de 264 ciclos por segundo.
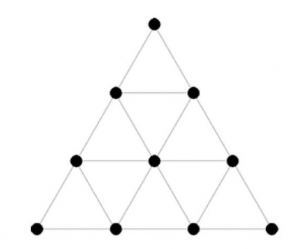
La clave para las proporciones armónicas se encuentra escondido en la tetraktis de Pitágoras. La tetraktis está formada por 4 números cuyas proporciones expresan los espacios de la octava.
Para Pitágoras, la música constituía una de las partes de la divina ciencia de las matemáticas y sus armonías eran verificadas por proporciones matemáticas. Además, los Pitagóricos afirmaban que las matemáticas mostraban el método exacto mediante el cual Dios había creado el universo y lo mantenía.
Pitágoras dividió las partes de la creación en esferas. A cada una de ellas atribuía un tono, un espacio armónico, un color, un número y una forma. Para demostrar la exactitud de sus conclusiones, relacionó estas esferas con los diversos planos del espíritu y de la materia, los cuales iban graduándose desde la estructura lógica más abstracta hasta el cuerpo geométrico más denso. Aplicó la recientemente descubierta ley de los espacios armónicos a todos los fenómenos de la naturaleza, mostrando la relación armónica de los planetas y las constelaciones entre sí. Un notable ejemplo de la demostración actual de estas antiguas enseñanzas filosóficas es la progresión de los elementos en proporciones armónicas. Confeccionando una lista de elementos en serie ascendente, de acuerdo a su peso atómico, Newlands descubrió en cada elemento octavo, una repetición de sus componentes. Este descubrimiento es conocido en la química actual como “ley de la octava”.
La “Coma pitagórica”
Todo comienza con el intento de Pitágoras y de sus discípulos de dividir la octava (diapasón) de una manera determinada, creando así una serie espacial de tonos, semitonos y de divisiones aun más pequeñas que el semitono, dando como resultado la aparición de las escalas. Es decir, aquello que los antiguos llamaban sistema y que hoy denominamos escalas. Podemos calcular la Coma pitagórica de la siguiente manera:
Comenzando con un Do de piano y avanzando con quintas, tenemos:
Do 1 3/2 = sol 1. 3/2 = re 2. 3/2 = la 2. 3/2 = mi 3. 3/2 = si 3. 3/2 =
fa# 4. 3/2 = do 5#. 3/2 =
= sol# 5. 3/2 = re 6#. 3/2 =
la 6 #.3/2 = mi # 7.3/2 = si 7#.
(los indicadores 1, 2, 3… indican la serie de la octava)
Con 1 el primer do de la serie tendremos:
si # 7 / do 1 = (3/2)12 (a)
Si ahora comenzamos y avanzamos con espacios de octava (2:1), entonces en vez de si 7# encontraremos lógicamente los do 8 que tendrá que estar en proporción con el do 1: do 8 / do 1 = 27 (b)
La diferencia entre estas dos razones (a y b) nos da lo que llamamos la coma pitagórica, una diferencia acústica muy pequeña, claro, pero capaz de alterar la certitud
sobre las proporciones perfectas e íntegras que buscaban los Pitagóricos.
Una diferencia del tenor:
(3:2)12 / 27 = 312 / 210 = 1,0136406<1/4 del tono.
Así pues, en un instrumento musical, si mantenemos las quintas de manera correcta, descomponemos las octavas y viceversa.
El reloj interno del hombre y la “Coma pitagórica”
(Novedades científicas, revista Science, mayo 2000)
Steven Reppert y sus colaboradores de la Facultad de Medicina de Harvard encontraron datos sobre el mecanismo que dirige los genes a través de las proteínas, de
manera que pueda ser regulado el reloj interno de un ser biológico, durante el ciclo de sueño y vigilia.
Mientras que normalmente habríamos esperado que este ciclo fuese de 24 horas, como es el ciclo del día, sin embargo comprobamos que el período de este ciclo es de 24 horas y 11 minutos. Este período exacto fue medido por primera vez en 1999 por Charles Czeizler, también de la Facultad de Medicina de Harvard. Si dejásemos que nuestro reloj biológico funcionase solo, avanzaríamos cada día 11 minutos más que el día anterior (24 horas).
 También aquí aparece la idea de la “coma” pitagórica porque, mientras que el ciclo del día es de 24 horas, o sea de 1440 minutos, la duración del reloj biológico es de1451 minutos. Y 1451/1440 = 1,007638, un número que se acerca mucho a la coma pitagórica (1,0136406). En estos números, en base a los instrumentos deexperimentación y de investigación de los que disponemos, la exactitud es algo inaccesible. Por ejemplo, la duración del día no es exactamente 24 horas sino un poco más y oscila en los grandes ciclos astronómicos. De la misma manera, es probable que la medida del reloj biológico interno no sea exacta. Por lo tanto, esta diferencia en los números no es suficientemente clara.
También aquí aparece la idea de la “coma” pitagórica porque, mientras que el ciclo del día es de 24 horas, o sea de 1440 minutos, la duración del reloj biológico es de1451 minutos. Y 1451/1440 = 1,007638, un número que se acerca mucho a la coma pitagórica (1,0136406). En estos números, en base a los instrumentos deexperimentación y de investigación de los que disponemos, la exactitud es algo inaccesible. Por ejemplo, la duración del día no es exactamente 24 horas sino un poco más y oscila en los grandes ciclos astronómicos. De la misma manera, es probable que la medida del reloj biológico interno no sea exacta. Por lo tanto, esta diferencia en los números no es suficientemente clara.
La “Coma pitagórica” y su importancia metafísica
Esta pequeña disonancia o imperfección, la coma pitagórica, es la base de la existencia del mundo. Si no existiera esta pequeña imperfección, el mundo no existiría.
Existiría una armonía estática, reabsorbida en una perfección infinita.
 De la misma manera que el corazón no se encuentra en el centro del pecho, que el eje de la tierra noes totalmente vertical en su órbita y de la misma manera que el año solar no coincide con el año lunar, así también el desarrollo de las 12 quintas, en vez de llevarnos de nuevo al principio de la octava, nos deja una diferencia ínfima, la “coma”, la cual debemos trascender, y es la que hace que cualquier cálculo sea complejo, que nos sea difícil configurar esas leyes severas pero simples, atractivas pero imprecisas, con las que se deleita nuestra mente. Estas “quintas” conforman una espiral en la que las notas, volviendo sobre sí mismas, no pueden encontrarse nunca. Para nosotros, esta espiral infinita puede ser el punto en la estructura del mundo, la estrecha puerta que nos permitirá escaparnos de la apariencia de un universo cerrado, viajar a otros mundos y explorar sus misterios.
De la misma manera que el corazón no se encuentra en el centro del pecho, que el eje de la tierra noes totalmente vertical en su órbita y de la misma manera que el año solar no coincide con el año lunar, así también el desarrollo de las 12 quintas, en vez de llevarnos de nuevo al principio de la octava, nos deja una diferencia ínfima, la “coma”, la cual debemos trascender, y es la que hace que cualquier cálculo sea complejo, que nos sea difícil configurar esas leyes severas pero simples, atractivas pero imprecisas, con las que se deleita nuestra mente. Estas “quintas” conforman una espiral en la que las notas, volviendo sobre sí mismas, no pueden encontrarse nunca. Para nosotros, esta espiral infinita puede ser el punto en la estructura del mundo, la estrecha puerta que nos permitirá escaparnos de la apariencia de un universo cerrado, viajar a otros mundos y explorar sus misterios.
Sin la “coma” no podemos hacer nada de eso. El hombre ha extraído su música del mar de la existencia, el constante vibratorio y las concordancias preexisten ya dentro de los mecanismos de las olas y de las frecuencias. No descubrimos nada. Sencillamente podemos sentir esos ritmos y esas fuerzas cósmicas y corresponder a ellas, porque también nosotros vibramos al compás de estos ritmos.
El hombre debe aprender a conciliarse con las armonías de su medio. La música es el puente entre lo manifestado y lo invisible. Lo que se muestra ante nuestros
sentidos no es sino una presencia externa, un cascarón de las energías más profundas. Detrás se esconde algo muy grande, que queda a la espera de su interpretación.
La música y las matemáticas
Ianis Xenakis – La entrevista que se refiere a continuación fue dada en septiembre de 1978, cuando vino a Micenas y presentó el “Poliespacio de Micenas” La música es quizás el arte más ligado a las matemáticas, al pensamiento matemático, en razón de su propia naturaleza. Su estructura ordenadora puede disponer los elementos de un conjunto, de un caracter, como ser la altura, la intensidad, la densidad, o como ser el grado de desorden. A través de la historia, en muchas ocasiones el pensamiento musical fue una vanguardia frente al pensamiento matemático. Los Pitagóricos, por ejemplo, relacionaban la altura con la longitud de las cuerdas. Por ejemplo, para encontrar el espacio de la octava, tenían que dividir la cuerda en cuatro. Es una división con dos – se trata de una progresión geométrica regresiva.
 Aristoxenos de Tarento, desde el punto de vista de los músicos, decía las mismas cosas aunque de manera diferente. Para hacer doble un espacio de octavas, sencillamente tengo que añadir un espacio, un espacio musical, de otra octava. Por lo tanto, lo que Pitágoras
Aristoxenos de Tarento, desde el punto de vista de los músicos, decía las mismas cosas aunque de manera diferente. Para hacer doble un espacio de octavas, sencillamente tengo que añadir un espacio, un espacio musical, de otra octava. Por lo tanto, lo que Pitágoras
llamaba multiplicación, Aristoxenos, que era músico, lo llamaba adición. Ahora bien, en cuanto a la relación que existe, punto por punto, entre la altura de volumen que escuchamos y la longitud de la cuerda del instrumento físico que produce el sonido, esta relación no la habían observado en aquella época, a pesar de que la ponían en práctica. Como teoría matemática la encontramos mucho después. Es la llamada función logarítmica o su inversión, la función exponencial. He aquí un ejemplo en el que los músicos habían expresado determinados puntos de vista dos mil años antes de lo que lo expresaran las matemáticas.
Ritmo – Número
Garland y Kahn (1995) señalan que se considera ya demostrado el hecho de que las primeras creaciones musicales son anteriores a la palabra hablada. El hallazgo más antiguo, con relación a las costumbres musicales del hombre, ha sido datado en 35.000 años y es un conjunto de huesos de mamut los cuales, según la opinión de los arqueólogos, fueron utilizados para producir sonidos aparentemente rítmicos. Así pues, el ritmo es el primer tipo de música que utilizó el hombre.
Refiriéndonos ahora al terreno de las matemáticas, el primer concepto matemático que comenzó a crearse en la mente del hombre desde muy antiguo, es el número. Este punto de vista tiene un sólido fundamento, que deriva del estudio sobre la manera en que el niño desarrolla gradualmente el concepto de número, ya desde la edad preescolar. Investigadores actuales como Gelman y Gallistei (1982) afirman que la primera capacidad del niño y la más elemental, en relación a las matemáticas, es la de la enumeración. El niño, a través de su capacidad innata de dividir el tiempo, crea una equivalencia 1 – 1 de los acontecimientos con los momentos de tiempo, es decir que en esencia está numerando. Lo mismo afirma D. Tall (1991) cuando refiere que el niño en principio numera sin tener concepto del número. Esto es evidente a causa de los errores que hace el niño, del tenor: uno, dos, tres, siete,… errores que son interpretados con la hipótesis de que el niño al principio utiliza sencillamente los nombres de los números, que coloca en una equivalencia 1 – 1 con los momentos en que los pronuncia. (Nota: O. Wilder (1986) afirma que la enumeración constituye una necesidad cultural, un elemento universal de civilización. La enumeración parece conducir al concepto de número a través de la utilización de símbolos, que en principio representaban de manera simple y visual el proceso de la enumeración | para el 1, || para el 2, ||| para el 3 y esto nos presenta un serio indicio de la evolución común del hombre hacia las ideas del número y del ritmo). En resumen, podemos ya afirmar con una buena base, que los dos conceptos fundamentales y primarios del ritmo y del número tienen un origen común que provienen de la división del tiempo, a través de la creación de intervalos en su duración, y de la equivalencia 1 – 1.
Lo más notable es que también los filósofos Chinos de la época de Confucio consideraban los números pequeños 1, 2, 3, 4 como la esencia de la perfección (J. Jeans
1968). Euler, en 1738, intenta dar una explicación sobre el origen de la armonía. Tenemos, dice Euler, una tendencia innata a sentir satisfacción cuando descubrimos una regularidad o una ley. La regularidad más simple, por lo tanto la más fácil de apreciar, es la que se basa en las razones de los números simples 1, 2, 3, 4 (J. Jeans, 1968). En esencia, Euler está de acuerdo con el punto de vista pitagórico y lo sustenta en una base más realista.
Sobre la armonía
 El problema de Fibonacci, que se relaciona con el número de la sección áurea de Pitágoras, lo encontramos en toda la naturaleza viva, en las espirales vivas. La serie de Fibonacci, así como los llamados números transcendentales (el número F de la sección áurea, el p, el e neperiano y también ahora el número “de la globalidad” de Feigenbaum sobre el paso de los sistemas al estado de caos) son tales que para calcular cualquier número de la serie es imprescindible que conozcamos el anterior.
El problema de Fibonacci, que se relaciona con el número de la sección áurea de Pitágoras, lo encontramos en toda la naturaleza viva, en las espirales vivas. La serie de Fibonacci, así como los llamados números transcendentales (el número F de la sección áurea, el p, el e neperiano y también ahora el número “de la globalidad” de Feigenbaum sobre el paso de los sistemas al estado de caos) son tales que para calcular cualquier número de la serie es imprescindible que conozcamos el anterior.
 No existe ninguna fórmula matemática que nos dé la posibilidad de preverlos. Diríamos, de manera simbólica, que están “colgados” desde el cielo, en el mundo Arquetípico, entre el cielo y la tierra y, por esa razón, son divinos y
No existe ninguna fórmula matemática que nos dé la posibilidad de preverlos. Diríamos, de manera simbólica, que están “colgados” desde el cielo, en el mundo Arquetípico, entre el cielo y la tierra y, por esa razón, son divinos y
transcendentales.
Los números como arquetipos y como realidades psicológicas. Psicología de Jung
Marie-Louise von Franz (del Instituto de C. Jung en Zurich) ha escrito un estudio sobre la importancia del número en las matemáticas, en la filosofía y como símbolo de valor psicológico, en un intento de conciliar la distancia existente entre la psicología y la física. Observó que Niels Bohr había subrayado el hecho de que se ha realizado un gran adelanto en la concienciación de que la descripción de la realidad puede hacerse por medio de la combinación de números puros, cosa que se hace eco del sueño de la escuela pitagórica.
Los números parecen representar características de la materia y al mismo tiempo representan también los fundamentos inconscientes de los procesos mentales. Por esa razón, de acuerdo a C. Jung, el número conforma ese elemento concreto que unifica el reino de la materia con el del alma. Es “real” en un doble sentido, como una imagen arquetípica y como una expresión cuantitativa en el reino de la experiencia externa. Por lo tanto, el número tiende un puente entre el mundo físico conocido y el mundo de la imaginación. De esta manera, se convierte en agente de unión, mediador entre el mito y la realidad, a la vez cualitativo y cuantitativo, expresivo e inexpresivo.
Los números, sobre todo como estructuras arquetípicas estables del inconsciente grupal, poseen un aspecto dinámico y activo que es de fundamental importancia para la mente. Lo esencial no el qué podemos hacer nosotros con los números, sino el qué hacen los números en nuestra conciencia.
Cuando estudiamos las características específicas de los números físicos, podemos destacar que ellos generan los mismos resultados reguladores al nivel físico y al psíquico. Así parecen constituir las constantes más básicas de la naturaleza, expresando la realidad psicofísica de manera unificada. En razón de todo lo expresado, deducimos que la misión de los matemáticos del futuro será la de reunir las características de los números y analizar cada número en su relación lógica con todos
los demás, cuando ello sea posible. Esta investigación podría ser asignada a los matemáticos en colaboración con los físicos, los músicos, los psicólogos, que son
conocedores de los hechos experimentales en relación a las características estructurale de los números en los diversos campos.
Si realmente el número, y las matemáticas en general, reflejan el orden del Mundo Uno (unus mundus), esto podría explicar el gran misterio de que las matemáticas, aunque son un fenómeno de la mente, se revelan tan extraordinariamente eficaces en la representación del mundo físico. Esta misteriosa armonía entre el alma y la materia está, sin ninguna duda, presente en los fundamentos de la física y demuestra las raíces pitagóricas de la Física actual. Los quantas, al igual que los números, tienen dos aspectos complementarios, que son imprescindibles si queremos comprenderlos de manera más completa. Estos dos elementos tienen aspectos cuantitativos y cualitativos, a la vez estáticos y dinámicos.
“A fin de cuentas, el misterio del unus mundus se encuentra en la naturaleza delnúmero” (Marie-Louise von Franz, Number and Time: Reflections Leading toward a Unification of Depth Psychology and Physics, Enanston: Northwestern University Press, p. 54)
Matemáticas, el secreto del universo
 Podemos considerar a las matemáticas, siguiendo a Pitágoras, nada menos que el secreto del universo. Desde la época de Galileo los científicos han descubierto que no sólo los fenómenos físicos pueden ser captados por las matemáticas, sino que el mundo mismo parece tener un carácter matemático. Galileo denominaba a las matemáticas “lenguaje de la naturaleza” y Sir Arthur Eddington decía que el estudio de la física nos da “el conocimiento de las estructuras matemáticas”. El universo físico, con todas sus diferenciaciones, puede ser descrito con toda exactitud en términos de unas relativamente pocas ecuaciones.
Podemos considerar a las matemáticas, siguiendo a Pitágoras, nada menos que el secreto del universo. Desde la época de Galileo los científicos han descubierto que no sólo los fenómenos físicos pueden ser captados por las matemáticas, sino que el mundo mismo parece tener un carácter matemático. Galileo denominaba a las matemáticas “lenguaje de la naturaleza” y Sir Arthur Eddington decía que el estudio de la física nos da “el conocimiento de las estructuras matemáticas”. El universo físico, con todas sus diferenciaciones, puede ser descrito con toda exactitud en términos de unas relativamente pocas ecuaciones.
Desde entonces han pasado tantos siglos y la belleza de las grandiosas reflexiones de los Pitagóricos continúa viva y sigue llenándonos de admiración. Por esa razón, cuando hablamos de Pitágoras, entendemos la síntesis del espíritu griego, la síntesis de la belleza con la ciencia y con la teología, de Apolo con Dionisos.
Bibliografía
«SCIENCE AND MUSIC», James Jeans, (Dover 1968)
«PITAGORAS», G. Sakelariou, (1963)
«LA EVOLUCION DE LOS CONCEPTOS MATEMATICOS», (Open University 1986)
«PITAGORAS Y LA DOCTRINA SECRETA DEL PITAGORISMO», P. Gravinger, (Ideotheatron, 1998)
«LA CIFRA TEORICA DE LOS PITAGORICOS», Thomas Taylor, (Jamblico, 1995)
http://www.telemath.gr/mathematical_articles/mathematical_articles_music/maths_artic les_music.php
http://www.scribd.com/doc/30814991/Thomas-Taylor
http://www.aoratos-naos.com/t292-topic
http://www.scribd.com